Picture this: you’re staring at a daunting trigonometry problem, a web of angles and sides, and the question “Find the value of each trigonometric ratio” stares back at you. It can feel like you’re trying to navigate a dense forest without a compass. Fear not! This comprehensive guide will be your trusty compass, leading you through the intricacies of trigonometric ratios and equipping you with the knowledge to confidently answer any question thrown your way.
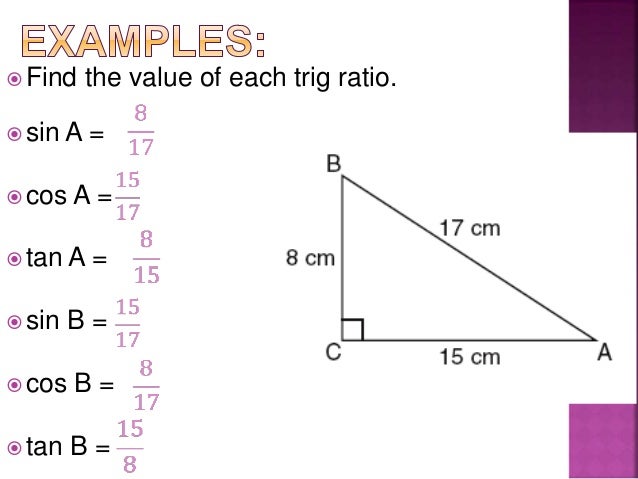
Image: www.slideshare.net
Trigonometry, the study of triangles, is a powerful tool in mathematics, reaching beyond the classroom into real-world applications like architecture, engineering, and even navigation. Understanding trigonometric ratios is the key to unlocking the secrets of this fascinating field. These ratios, sine, cosine, and tangent, are like the DNA of a triangle, giving us the power to decipher its hidden characteristics.
Delving Deeper into the World of Trigonometric Ratios:
Let’s begin our journey by understanding the fundamental building blocks:
1. The Right Triangle: Our Stage
Trigonometric ratios are defined for right-angled triangles. Imagine a right triangle, with one angle measuring 90 degrees. This triangle is our canvas, and the sides are our paintbrush.
2. Identifying the Sides:
- Hypotenuse (H): The longest side of the right triangle, always opposite the right angle. Think of it as the triangle’s backbone.
- Opposite (O): The side across from the angle we’re interested in. It’s the side that ‘faces’ the angle.
- Adjacent (A): The side next to the angle we’re studying, excluding the hypotenuse. Think of it as the side ‘adjacent’ or ‘neighboring’ the angle.
3. The Trigonometric Ratios: Sine, Cosine, and Tangent
Now, let’s define the three main trigonometric ratios:
- Sine (sin): Defined as the ratio of the opposite side to the hypotenuse: sin θ = Opposite / Hypotenuse (O/H)
- Cosine (cos): Defined as the ratio of the adjacent side to the hypotenuse: cos θ = Adjacent / Hypotenuse (A/H)
- Tangent (tan): Defined as the ratio of the opposite side to the adjacent side: tan θ = Opposite / Adjacent (O/A)
Remember the mnemonic “SOH CAH TOA” to help you recall these ratios:
SOH: Sine = Opposite / Hypotenuse
CAH: Cosine = Adjacent / Hypotenuse
TOA: Tangent = Opposite / Adjacent
Finding the Value of Each Trigonometric Ratio: A Step-by-Step Guide
Now that we’ve established the foundation, let’s move on to the practical implementation. Here’s a step-by-step approach to finding the value of each trigonometric ratio:
-
Identify the Angle: Start by identifying the angle (θ) for which you want to find the trigonometric ratios.
-
Label the Sides: Label the sides of the right triangle as hypotenuse (H), opposite (O), and adjacent (A) in relation to the chosen angle (θ).
-
Apply the Ratios: Use the SOH CAH TOA mnemonic to determine the appropriate ratio for each trigonometric function:
- sin θ = O/H
- cos θ = A/H
- tan θ = O/A
-
Substitute and Calculate: Substitute the values of the opposite, adjacent, and hypotenuse sides into the relevant ratio and calculate the result.
Real-World Examples: Where Trigonometry Shines
Trigonometry isn’t just confined to textbook problems. It plays a crucial role in various real-world scenarios:
- Engineering: Engineers use trigonometry to calculate forces, stresses, and strains in structures like bridges and buildings. Understanding the forces acting on different angles is crucial for ensuring stability and safety.
- Navigation: Sailors and pilots rely on trigonometry to determine their position, calculate distances, and chart courses. By understanding the angles and distances involved, they can navigate effectively across oceans and skies.
- Architecture: Architects use trigonometry to design and construct buildings, ensuring structural integrity and aesthetic appeal. From roof angles to staircase designs, trigonometry shapes our built environment.
- Surveying: Surveyors use trigonometric principles to measure distances, elevations, and angles, creating accurate maps and plans for various projects.
Image: www.hotzxgirl.com
Mastering Trigonometric Ratios: Tips and Tricks
Here are some valuable tips to help you master trigonometric ratios:
- Practice, Practice, Practice: The key to becoming proficient is consistent practice. Solve numerous problems, gradually increasing the complexity, to develop a deep understanding.
- Visualize: Draw the triangles and label the sides clearly to visualize the relationships between the angle, opposite, adjacent, and hypotenuse.
- Use a Calculator: Utilize a scientific calculator to efficiently calculate trigonometric ratios for different angles.
- Apply the Unit Circle: The unit circle is a powerful tool for visualizing trigonometric values and understanding their relationships.
Find The Value Of Each Trigonometric Ratio Answer Key
Conclusion: Embracing the Power of Trigonometry
Learning to find the value of each trigonometric ratio is the first step towards harnessing the immense power of trigonometry. From solving complex mathematical problems to navigating through the real world, this knowledge empowers you to understand and analyze a wide range of situations. So, embrace the learning journey, explore its applications, and let trigonometry unlock a world of possibilities. Remember, the key to mastering any subject lies in curiosity, dedication, and a thirst for knowledge.






